Rapid Dynamic Analysis Engine

QUAKE ADVICE_Seismic Analysis by Generalised Force Method (GFM)

Seismic Analysis by Rapid Dynamic Analysis (RDA)

1. Input Parameters:

Specify if the building has any setback or podium features:

A. Upload the Building’s Floor Plan (for the Typical Floor):

A. Upload the Building’s Floor Plan (for the Storey Below the Setback Level):

A. Upload the Building’s Floor Plan (for the Storey Above the Podium Level):

The dymamic analysis is achieved based on the input of the floorplan of the building (drawn to scale). Please upload floor plan (any image file format) below.

Note: Any information outside the boundary of the floorplan and any written text within the floorplan need to be removed before uploading the image. Click ‘More Info’ button to see an example.

Upload Image File of the Building Floor Plan Here:

Input Length of the Red Rectangle along X-axis (in m):
Select The Direction of Loading:
Input Combination Percentages: &nbsp X-Direction:	Y-Direction:

Please verify the dimensions of the structural elements provided in the table below. If the displayed dimensions differ from the actual measurements, kindly update the values by specifying the correct information in the ‘Make Changes’ column.

Specify if any of the wall terminates at the setback or podium level:

Select the type of structural system from the following three options:

Slab Depth (in mm):
Characteristic Compressive Strength of Concrete (MPa):

Typical Interior Beam Dimensions(in mm):
W1:
W2:
D:

Typical Exterior Beam Dimensions(in mm):
W1:
W2:
D:

Typical span (beam spacing) in the orthogonal direction of motion (in m):

B. Details of the Building’s Elevation:

No. of Storeys:

Storey of Setback or Podium Level:

Define Seismic Mass:

Dead Load Density (kN/m³):
Floor Live Load Rating (kPa):

Note:

Please provide input for storey mass and height of the roof on the first row and follow the descending pattern up to the base.
Default floor seismic mass is calculated from the seismic weight density of 2.75 tonnes/m³
Default storey height with uniform floor to floor height of 3.2 m is used.
For user defined mass and height, the table can be filled manually or by performing a copy (CTRL+C) and paste (CTRL+V) of data from an Excel spreadsheet.

The mass for the storey above the setback or podium level must be adjusted to reflect changes in the floor area.

Storey No.	Mass (tonnes)	Height above Ground (m)

C. Define Code Elastic Seismic Response Spectrum:

Copy and paste or manually fill the code Response Spectral Acceleration (RSA) in ‘g’ for different periods. RSA is often represented as “k_p Z C_h(T₁) in AS1170.4, S_e(T) in EC8, and S_a(T) in ASCE 7″.

Period (s)	RSA in ‘g’

(The input storey mass and storey height above ground are shown in Table 2.)

2. Results:

2.1 2D Dynamic Solution Including Higher Modes of Vibration:

The dynamic solution of the seismic response of the building in 2-dimension (no torsion or rotation) is determined as per the following 3 steps.

Step 1. Determination of the mode shape (ϕ_j), modal period (T_j) and participation factor (&#915_j) of the first 3 modes of vibration:
The normalised mode shape, modal period, and the participitation factor for the first mode of vibration of the building is determined using the free undamped response of the Timoshenko Beam Model as shown in Eqs.(1-3), respectively. $$ {ϕ_{j=1}(x) = Ax^2 +(1-A)x^3}\tag{1a}$$ $$ {A = 0.00007p^3+0.0006p^2-0.0095p-0.5}\tag{1b}$$ $${T_{j=1} = \left(\frac{2\pi}{B}\right) \times \sqrt{{\frac{M_{total}H^3}{(1+p^2)EI}}}}\tag{2a}$$ $$ {B = (0.36p^4-2.93p^3+6.43p^2-0.57p+187.55)/100}\tag{2b}$$ $$ {\Gamma_{j} = \frac{\sum^n_{i=1} (m_{i} ϕ_{j})}{\sum^n_{i=1}(m_{i} ϕ^2_{j})}}\tag{3}$$ where: p is the square root of the shear to flexural stiffness ratio calculated from the system type defined as an input; and M_total, H, and EI are the total mass, height, and flexural rigidity of the building.

For the second and third modes of vibration, the normalised mode shapes are obtained from Table A, and the corresponding periods are calculated by multiplying the first mode period by the period ratios provided in Table B.

Table A. Normalised mode shape for the higher modes.

x	1	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1
ϕ_j=2(x)	1	0.584	0.121	-0.315	-0.656	-0.856	-0.897	-0.784	-0.557	-0.271
ϕ_j=3(x)	1	0.240	-0.391	-0.675	-0.510	-0.019	0.503	0.754	0.616	0.236

Table B. Period ratios.

p	0.1	1	2.5	3.5	4.5	6.0	10	20
T_j=2/T_j=1	0.16	0.18	0.24	0.26	0.28	0.29	0.31	0.33
T_j=3/T_j=1	0.06	0.07	0.09	0.11	0.12	0.14	0.17	0.19

Step 2. Determination of the effective modal mass (M_j) and modal participation ratio (MPR_j) $$ {M_{j} = \sum^n_{i=1}({m_{i}}\:{{Γ_{j}}\:\:{ϕ_{i,j}}})}\tag{4}$$ $$ {MPR_{j} = \frac{M_{j}}{M_{total}}}\tag{5}$$ Step 3. Determination of the combined storey and inter-storey drift, storey and base shear, and overturning moment
The combination of storey drift (δ_{i,3 modes}), inter-storey drift (θ_{i,3 modes}), storey shear (V_{i,3 modes}), base shear (V_{b,3 modes}), and total overturning moment (OM) of the first three modes of vibration are calculated using Eqs. (6-11). $$ {δ_{i,3\:modes} = \sqrt{\sum^3_{j}{\left({{Γ_{j}}\:\:{ϕ_{i,j}}\:\:{RSD_{j}}}\right)}^2 }}\tag{6}$$ $$ {θ_{i,3\:modes} = \sqrt{\sum^3_{j}{\left(\frac{{{Γ_{j}}\:\:{(ϕ_{i,j}-ϕ_{i-1,j})}\:\:{RSD_{j}}}}{h_{i}}\right)}^2 }}\tag{7}$$ $$ {F_{i,3\:modes} = \sqrt{\sum^3_{j}{\left({m_{i}:\:{Γ_{j}}\:\:{ϕ_{i,j}}\:\:{RSA_{j}}}\right)}^2 }}\tag{8}$$ $$ {V_{i,3\:modes} = \sqrt{{\left(\sum^n_{i}{m_{i}}\:{{Γ_{1}}\:\:{ϕ_{i,1}}\:\:{RSA_{1}}}\right)}^2 + {\left(\sum^n_{i}{m_{i}}\:{{Γ_{2}}\:\:{ϕ_{i,2}}\:\:{RSA_{2}}}\right)}^2 + {\left(\sum^n_{i}{m_{i}}\:{{Γ_{3}}\:\:{ϕ_{i,3}}\:\:{RSA_{3}}}\right)}^2}}\tag{9}$$ $$ {V_{b,3\:modes} = \sqrt{{\left({V_{b,1}}\right)}^2+{\left({V_{b,2}}\right)}^2+{\left({V_{b,3}}\right)}^2}}\tag{10}$$ $$ {OM = \sum^n_{i=1}({{F_{i,3\:modes}} \times H_{i}})}\tag{11}$$ Where: RSA_j and RSD_j are the spectral acceleration and displacement of mode ‘j’ at ‘T_j‘, and h_i and H_i are the height of each storey ‘i’ and it’s height from the base of the building.

Table 1: Effective Modal Mass, Modal Participation Ratio, Effective Stiffness and Natural Period:

Figure 1: Normalised Mode Shape for the First Three Modes of Vibration

Figure 2: GFM Inter-Storey Drift

Figure 3: GFM Storey Shear

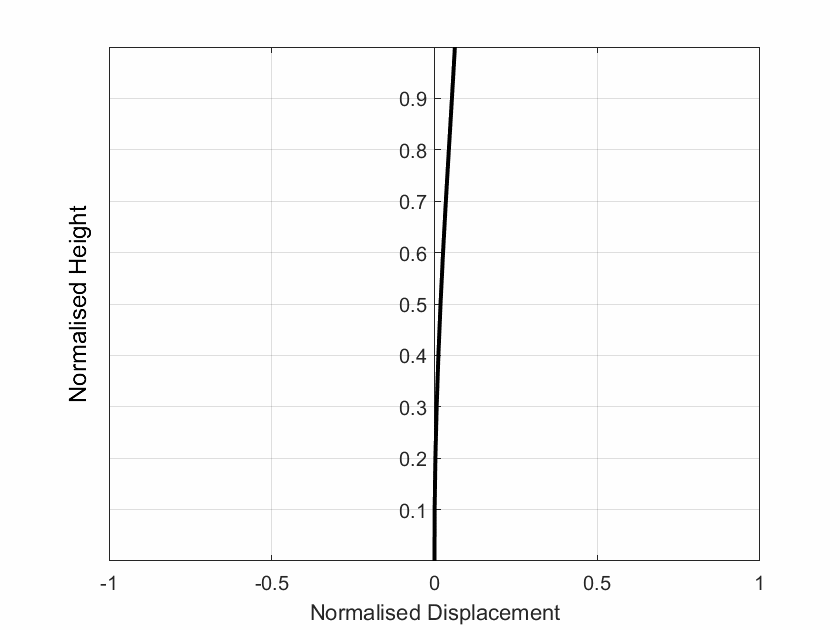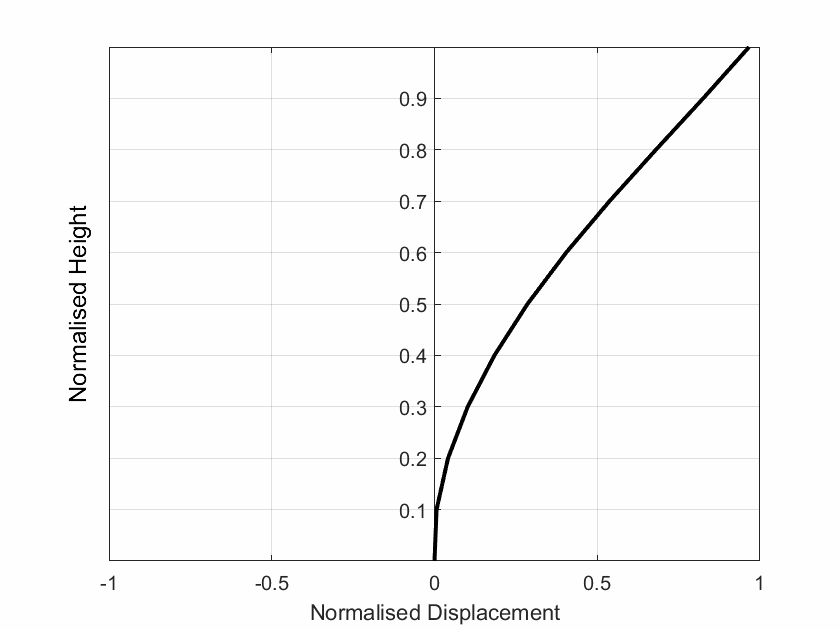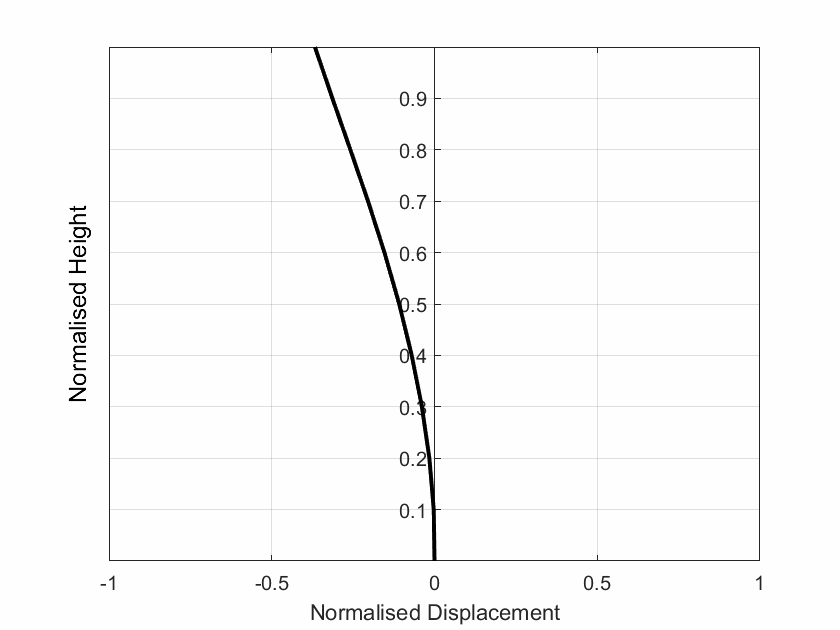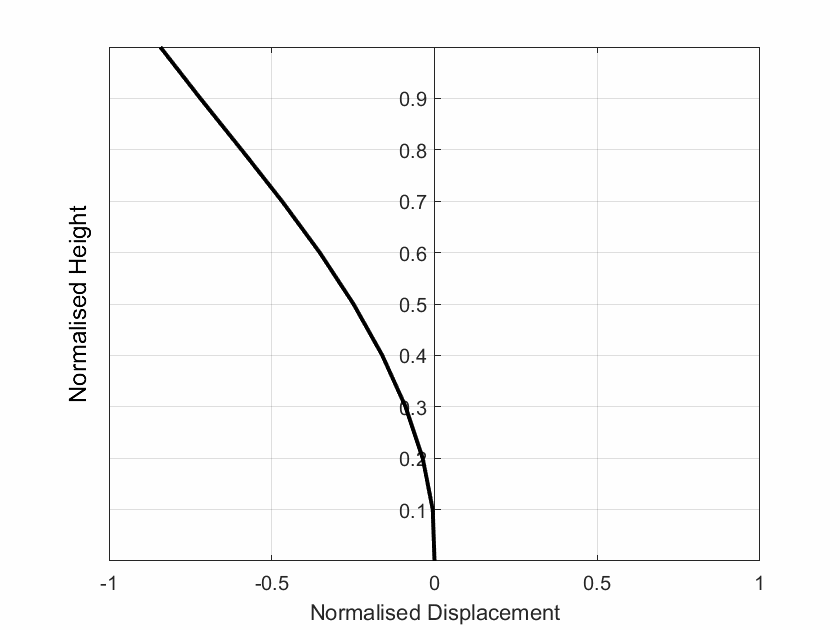
2.2 Solution Including 3D Torsional Amplification:

The floor plan of the building provided as an input is scanned here to determine the position of the centre of mass (CM) and centre of rigidity (CR) and the mass radius of gyration as shown in Figure 5. Then the torsional parameters such as the normalised elastic radius (br) and normalised eccentricity (er) are determined as per [1]. Finally, the 3D/2D displacement ratio is determined as per [2]. The torsional parameters and the 3D displacement profile is plotted against the 2D displacement in Figure 5.

Input Position of the Red Dot:

X-Coordinate:

Y-Coordinate:

Orientation Angle (degree):

Figure 4: Summary of the torsional parameters and the comparison of the 2D and 3D displacement profile.

Table 2: Summary of input information of the floor mass, height, and GFM results: floor displacements (δ_{i_GFM}), inter-storey drift (θ_{i_GFM}), inertia forces (F_{i_GFM}), storey shear (V_{i_GFM}), total base shear, and overturning moment.

4. References:

1. Khatiwada, P.; Lumantarna, E. Simplified Method of Determining Torsional Stability of the Multi-Storey Reinforced Concrete Buildings. CivilEng 2021, 2(2), 290-308.

2. Khatiwada, P.; Lumantarna, E.; Lam, N.; Looi, D. Fast Checking of Drift Demand in Multi-Storey Buildings with Asymmetry. Buildings 2021, 11, 13.

3. Standard, A. (2007). AS 1170.4-2007 (Amdt 2018).Structural Design Actions, Part 4: Earthquake Actions in Australia.

Disclaimer

The authors assume no responsibility for any injury, damage, liability, negligence and/or otherwise to any individual or property from the use or application of any of the methods, products, instructions, or ideas contained in the material herein.